Description,
There are N students in a class. Some of them are friends, while some are not. Their friendship is transitive in nature. For example, if A is a direct friend of B, and B is a direct friend of C, then A is an indirect friend of C. And we defined a friend circle is a group of students who are direct or indirect friends.

Given a N*N matrix M representing the friend relationship between students in the class. If M[i][j] = 1, then the ith and jth students are direct friends with each other, otherwise not. And you have to output the total number of friend circles among all the students.

Example 1:

Input: 
[[1,1,0],
 [1,1,0],
 [0,0,1]]
Output: 2

Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.
Example 2:

Input: 
[[1,1,0],
 [1,1,1],
 [0,1,1]]
Output: 1

Explanation:The 0th and 1st students are direct friends, the 1st and 2nd students are direct friends,
so the 0th and 2nd students are indirect friends. All of them are in the same friend circle, so return 1.
Note:
N is in range [1,200].
M[i][i] = 1 for all students.
If M[i][j] = 1, then M[j][i] = 1.

DFS in Java

Treat each student as a node, starting from the 0th student, using DFS to traverse all unvisted nodes (its direct friends).
img


public class Solution {
    public int findCircleNum(int[][] M) {
        int ret = 0;
        int[] visited = new int[M.length];
        for (int i=0; i<M.length; i++) {
            if (visited[i] == 0) {
                ret++;
                dfs(M, visited, i);
            }
        }
        return ret;
    }
    
    private void dfs(int[][] M, int[] visited, int i) {
        visited[i] = 1;
        for (int j=0; j<M.length; j++) {
            if (M[i][j] == 1 && visited[j] == 0) {
                dfs(M, visited, j);
            }
            
        }
    }
}

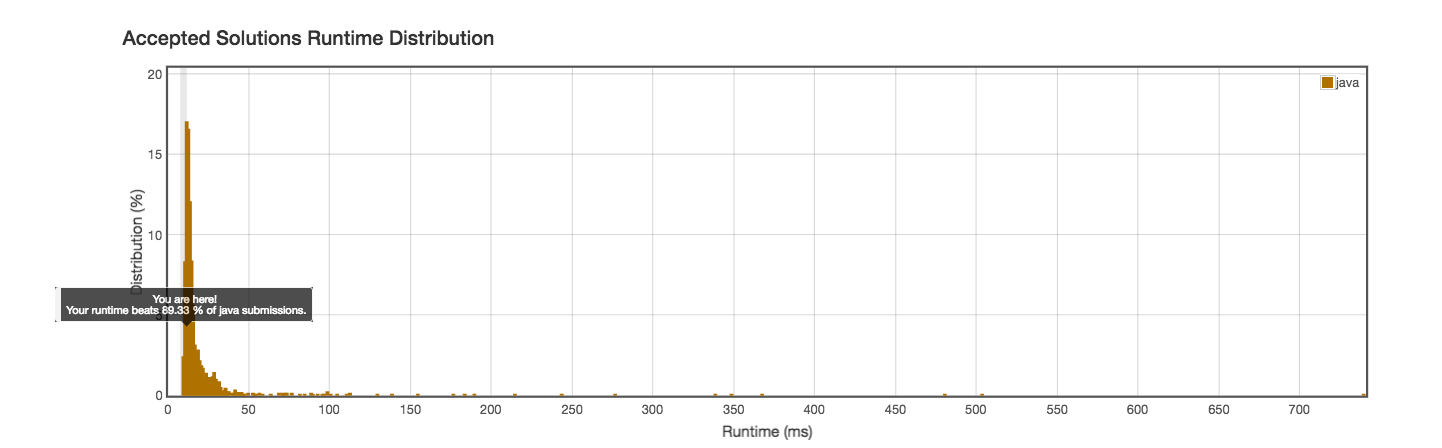imgRuntime: 10ms

another DFS in Python

This is a draft version of the DFS. The idea was to build the graph first, then apply DFS.
In fact, you do not need to. You can do the graph building via DFS and count the circle counting.


class Solution(object):
    def findCircleNum(self, M):
        """
        :type M: List[List[int]]
        :rtype: int
        """
        ret = 0
        hm = dict()
        for i in xrange(len(M)):
            for j in xrange(len(M)):
                group = hm.setdefault(i, set())
                if M[i][j] == 1:
                    group.add(j)
        #print hm
        allNodes = set()
        for i in xrange(len(M)):
            allNodes.add(i)
        while len(allNodes) != 0:
            ret += 1
            root = None
            for node in allNodes:
                root = node
                break
            self.dfs(root, set(), allNodes, hm)
            
        return ret        
        
    def dfs(self, root, visited, allNodes, hm):
        visited.add(root)
        allNodes.discard(root)
        unvisited = set()
        for node in hm.get(root):
            if node not in visited:
                unvisited.add(node)
        for node in unvisited:
            self.dfs(node, visited, allNodes, hm)

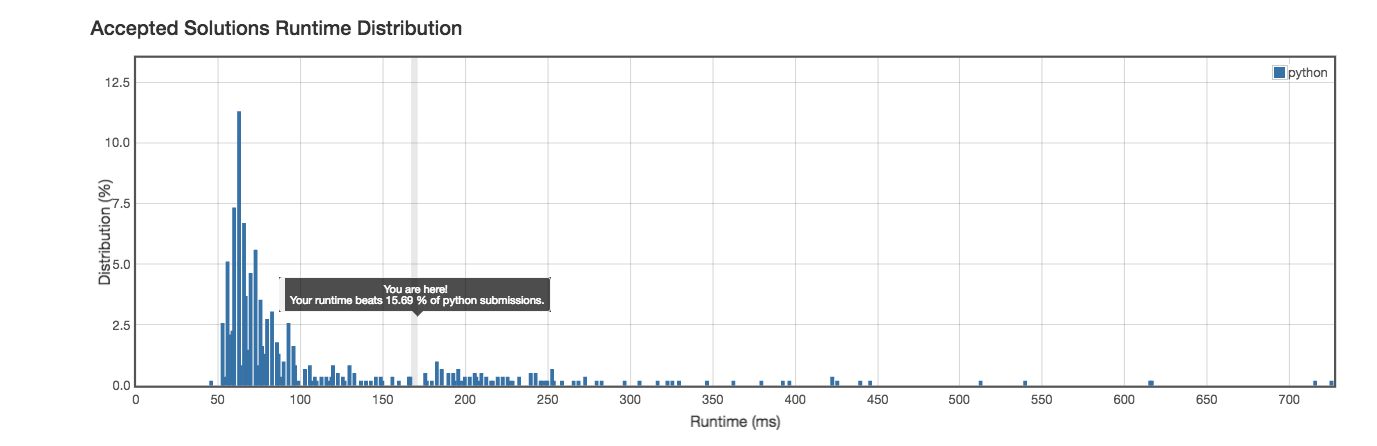imgRuntime: 169ms