Description,
A zero-indexed array A consisting of N different integers is given. The array contains all integers in the range [0, N - 1].

Sets S[K] for 0 <= K < N are defined as follows:

S[K] = { A[K], A[A[K]], A[A[A[K]]], … }.

Sets S[K] are finite for each K and should NOT contain duplicates.

Write a function that given an array A consisting of N integers, return the size of the largest set S[K] for this array.

Example 1:

Input: A = [5,4,0,3,1,6,2]
Output: 4
Explanation: 
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.

One of the longest S[K]:

S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}

Note:
N is an integer within the range [1, 20,000].
The elements of A are all distinct.
Each element of array A is an integer within the range [0, N-1].

Memorizing the circles solution

We consider a simple example and see how this problem can be resolved. From the figure below, we can see that the elements in the current nesting shown by arrows form a cycle. Thus, the same elements will be added to the current set irrespective of the first element chosen to be added to the set out of these marked elements.

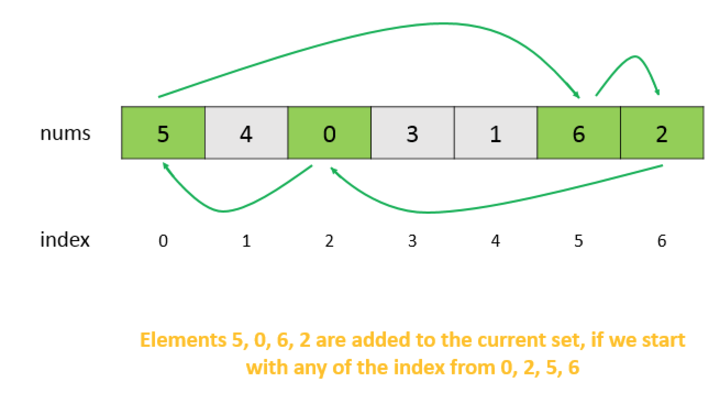imgmemorize the visited circles

Time complexity : O(n). Every element of the numsnums array will be considered atmost once.
Space complexity : O(1). Constant Space is used.
Note: if the array needs to be preserved, you should build auxiliary array to store the visited circles, which is O(n) space complexity.

public class Solution {
    public int arrayNesting(int[] nums) {
        int ret = Integer.MIN_VALUE;
        // boolean[] auxiliaryArrayForVisitedPos = new boolean[nums.length];
        for (int i=0; i<nums.length; i++) {
            if (nums[i] >= 0) {
                ret = Math.max(ret, buildAndCountSet(nums, i));
            }
        }
        return ret;
    }
    
    private int buildAndCountSet(int[] nums, int i) {
        int begin = i;
        int count = 0;
        do {
            count++;
            nums[i] = -nums[i];
            i = Math.abs(nums[i]);
        }
        while (i != begin);
        
        return count;
        
    }
}

imgRuntime: 40ms