Description,
Given the root of a tree, you are asked to find the most frequent subtree sum. The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself). So what is the most frequent subtree sum value? If there is a tie, return all the values with the highest frequency in any order.
Examples 1
Input:
5
/ \
2 -3
return [2, -3, 4], since all the values happen only once, return all of them in any order.
Examples 2
Input:
5
/ \
2 -5
return [2], since 2 happens twice, however -5 only occur once.
Post-order DFS with hashtable
Use post-order tree traversal to get the sum for each node.
Store the sums into one hashtable.
Note: you may track the largest sum during the traversal(my version does not do that, just for practicing the use of python’s dictionary setdefault() method :-)).
Time complexity: O(n)
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
import sys
class Solution(object):
def findFrequentTreeSum(self, root):
"""
:type root: TreeNode
:rtype: List[int]
:runtime: 75~95ms
:faster than: 80%~50% submissions.
"""
if not root:
return []
hm = dict()
self.dfs(root, hm)
ret = dict()
for k, v in hm.items():
lst = ret.setdefault(v, [])
lst.append(k)
max_val = -sys.maxint
for key in ret.keys():
if key > max_val:
max_val = key
return ret[max_val]
def dfs(self, root, hm):
"""
: @solution post-order DFS
: @return int int the sum of nodes of root.
"""
if not root:
return 0
left = self.dfs(root.left, hm)
right = self.dfs(root.right, hm)
if left+right+root.val not in hm:
hm[left+right+root.val] = 1
else:
hm[left+right+root.val] += 1
return left+right+root.val
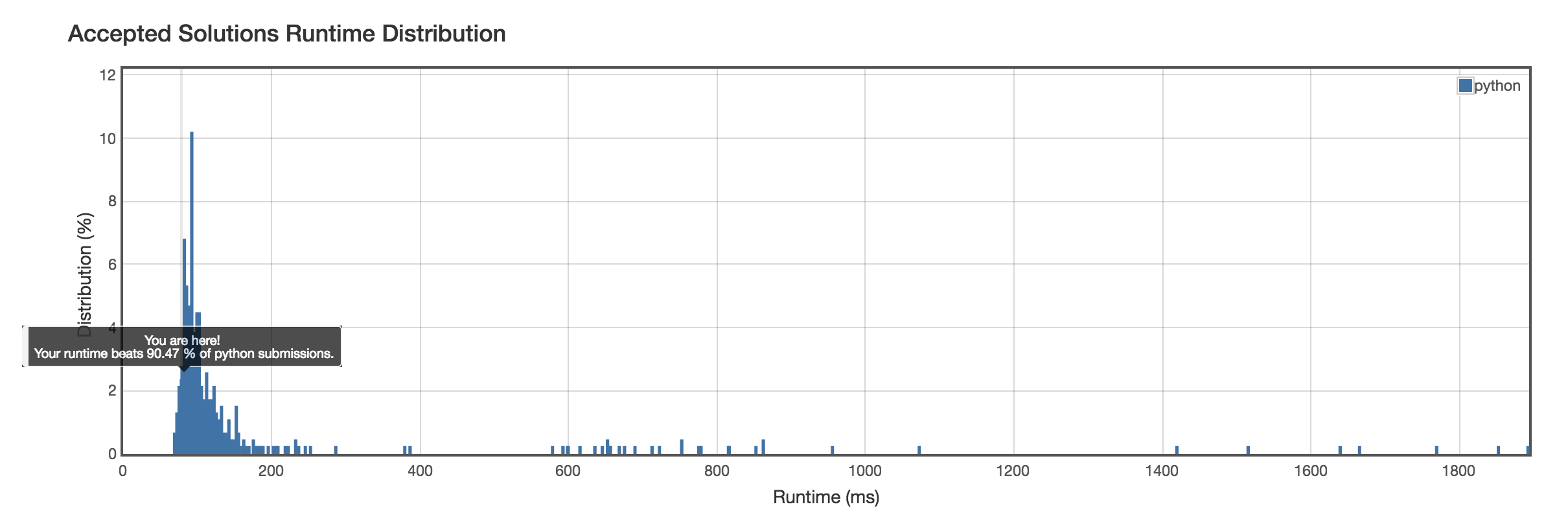 Runtime: 80ms
Runtime: 80ms