Description,
Implement strStr().

Returns the index of the first occurrence of needle in haystack, or -1 if needle is not part of haystack.

The leetcode link

KMP algorithm implemted in Java

Typically, the “find substring in string” problem could be efficiently solved by the Knuth–Morris–Pratt algorithm
Also, you can have detailed algorithm workthrough found here.
Interestingly, in Python, the str.find(‘substring’) is implemented by Boyer–Moore–Horspool algorithm, which is related to the KMP algorithm.

Time complexity: O(n + k)
RUntime: 13ms

public class Solution {
    /**
    * Return the starting index of the first needle found in haystack
    * @param  String haystack of type String
    * @param  String needle of type String
    * @return int the starting index 
    */
    public int strStr(String haystack, String needle) {
        int[] kmpTable= new int[needle.length()];
        buildKMPTable(needle, kmpTable);
        int i = 0;
        int j = 0;
        int N = haystack.length();
        int M = needle.length();
        while (i < N && j < M) {
            if (haystack.charAt(i) == needle.charAt(j)) {
                i++;
                if (++j == M) {
                   return i - j;
                } 
            } else {
                if (j == 0) {
                    i++;
                }
                else{
                    j = kmpTable[j-1];
                }
            } 
        }
        if (M == 0)   return 0; // when needle is null
        return -1;
    }
    
    /**
    * Returns the KMP table
    * @param  String needle
    * @param  int[] int[] to store the kmptable
    * @return void
    */
    private void buildKMPTable(String needle, int[] kmpTable) {
        int j = 0;
        int i = 1;
        while (i < kmpTable.length) {
            if (needle.charAt(i) == needle.charAt(j)) {
                kmpTable[i++] = ++j;
            } else {
                if (j == 0){
                    kmpTable[i++] = 0;
                } else {
                    j = kmpTable[j-1];
                }
            }
        }
        
    }
}

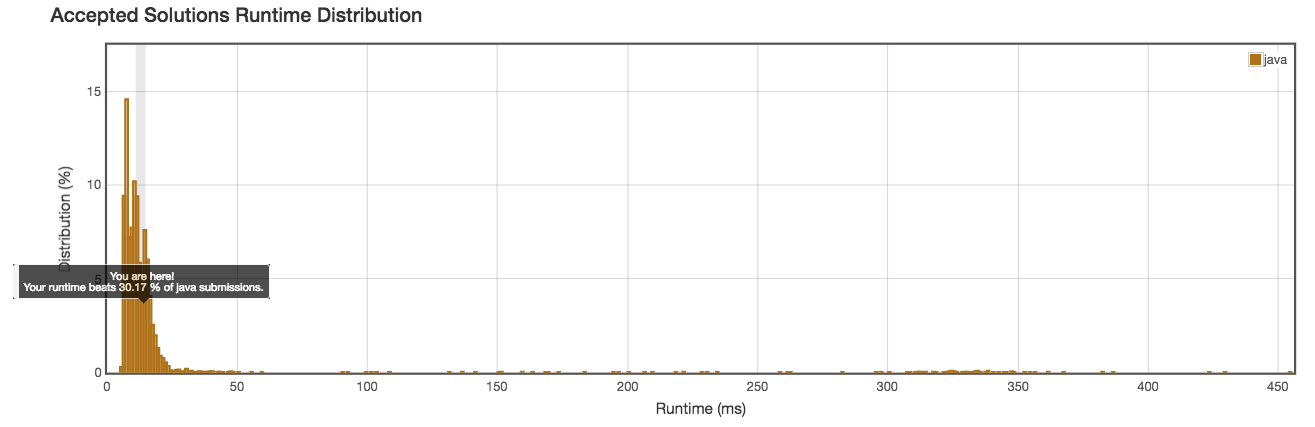imgRuntime: 13ms

Brutal algorithm in Python

This problem could also be solved brutal algorithms.

Time complexity: O(n^2)
Runtime: 38 ms

Note: the runtime looks okay just because leetcode’s unit test cases are simple.

class Solution(object):
    def strStr(self, haystack, needle):
        """
        :Find the substring in a brutal way.
        :type haystack: str
        :type needle: str
        :rtype: int
        """
        h, n = haystack, needle
        N = len(h)
        M = len(n)
        if M == 0: # edge case, when needle is "".
            return 0
        
        for i in xrange(N-M+1): # in case M > N, just return -1
            offset = i
            j = 0
            while j < M:
                if h[offset+j] != n[j]:
                    break
                j += 1
            if j == M:
                return i
            
        return -1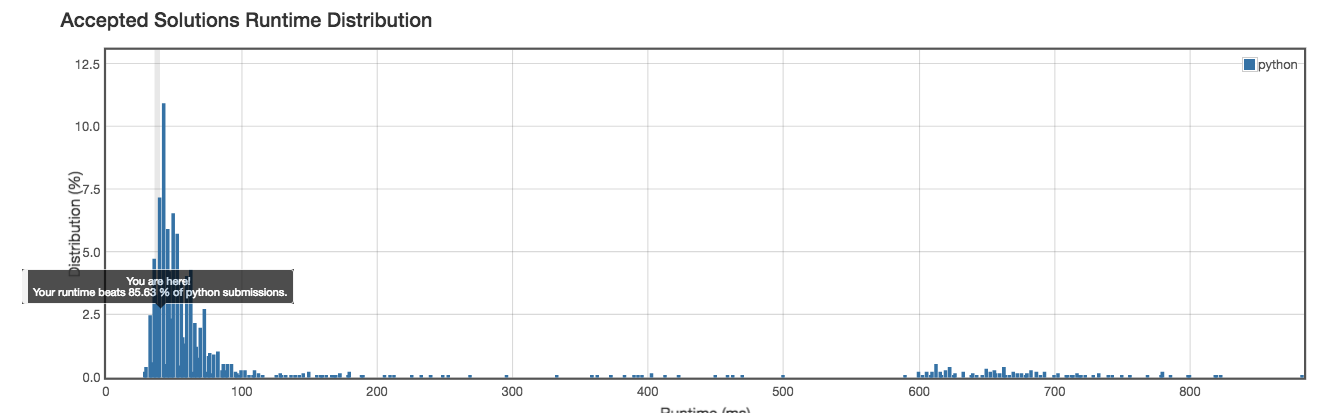

imgRuntime: 38ms