Description
Given two sparse matrices A and B, return the result of AB.
You may assume that A’s column number is equal to B’s row number.
Example:
A = [
[ 1, 0, 0],
[-1, 0, 3]
]
B = [
[ 7, 0, 0 ],
[ 0, 0, 0 ],
[ 0, 0, 1 ]
]
| 1 0 0 | | 7 0 0 | | 7 0 0 |
AB = | -1 0 3 | x | 0 0 0 | = | -7 0 3 |
| 0 0 1 |
Auxiliary Table Solution
Code below is a standard way of solving this problem.
A better solution inspired by one of the CMU lectures is here
public class Solution {
public int[][] multiply(int[][] A, int[][] B) {
boolean[] rowCheck = new boolean[A.length];
boolean[] colCheck = new boolean[B[0].length];
checkRow(rowCheck, A);
checkCol(colCheck, B);
int[][] ret = new int[A.length][B[0].length];
for (int i=0; i<A.length; i++) {
if (rowCheck[i]==false) continue;
for (int j=0; j<B[0].length; j++) {
if (colCheck[j]==false) continue;
for (int k=0; k<B.length; k++) {
ret[i][j] += A[i][k] * B[k][j];
}
}
}
return ret;
}
private void checkRow(boolean[] rowCheck, int[][] A) {
for (int i=0; i<A.length; i++) {
for (int j=0; j<A[0].length; j++) {
if (A[i][j] != 0) {
rowCheck[i] = true;
continue;
}
}
}
}
private void checkCol(boolean[] colCheck, int[][] B) {
for (int j=0; j<B[0].length; j++) {
for (int i=0; i<B.length; i++) {
if (B[i][j] != 0) {
colCheck[j] = true;
continue;
}
}
}
}
}
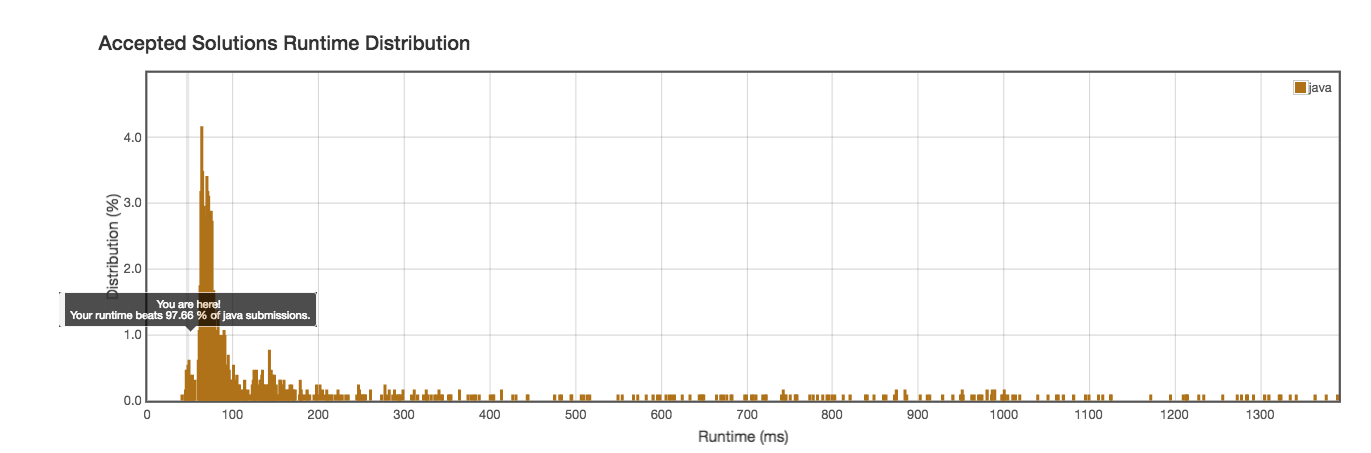 Runtime: 45-78ms
Runtime: 45-78ms