Description,
Given a binary array, find the maximum number of consecutive 1s in this array if you can flip at most one 0.

Example 1:
Input: [1,0,1,1,0]
Output: 4

Explanation: Flip the first zero will get the the maximum number of consecutive 1s.
After flipping, the maximum number of consecutive 1s is 4.

Note:

The input array will only contain 0 and 1.
The length of input array is a positive integer and will not exceed 10,000
Follow up:
What if the input numbers come in one by one as an infinite stream? In other words, you can’t store all numbers coming from the stream as it’s too large to hold in memory. Could you solve it efficiently?

Moving window solution

This algorithm is to maintain a moving window [low, i] that contains at most k zeros. And it could be using converted to cover the follow-up questions.

public class Solution {
    /**
    * Moving window that contains at most k zeros.
    * We can store the low in an ArrayList if the steam caannot be stored in RAM.
    * O(n) SpaceComplexity is O(n)
    */
    public int findMaxConsecutiveOnes(int[] nums) {
        int k = 1, low = 0, zeroCount = 0, ret = 0;
        for (int i=0; i<nums.length; i++) {
            if (nums[i] == 0) {
                zeroCount++;
            }
            while (zeroCount > k) {
                if (nums[low] == 0) {
                    zeroCount--;
                }
                low++;
            }
            ret = Math.max(ret, i - low + 1);
        }
        
        return ret;
    }
}

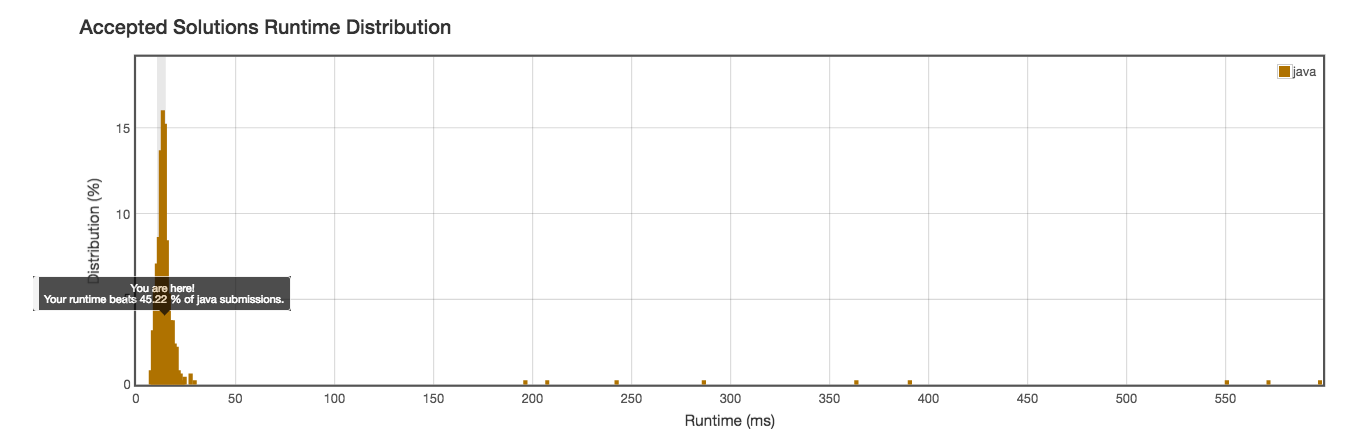imgRuntime: 13ms

Zero Divider Solution

The algorithm is not working for k > 1.
The idea is to only consider zeros whose prefix is 1 and suffix is also 1.

class Solution(object):
    def findMaxConsecutiveOnes(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        contiansZero = False
        ret = 0
        prevOnes = 0
        oneCount = 0
        for i in xrange(len(nums)):
            if nums[i] == 0:
                if not contiansZero:
                    contiansZero = True
                if i == 0 or nums[i-1] == 0:
                    prevOnes = 0
                else:
                    prevOnes = oneCount
                oneCount = 0 # reset one counting

            if nums[i] == 1:
                oneCount += 1
                ret = max(ret, prevOnes+oneCount)
        if contiansZero:
            return ret + 1
        else:
            return ret

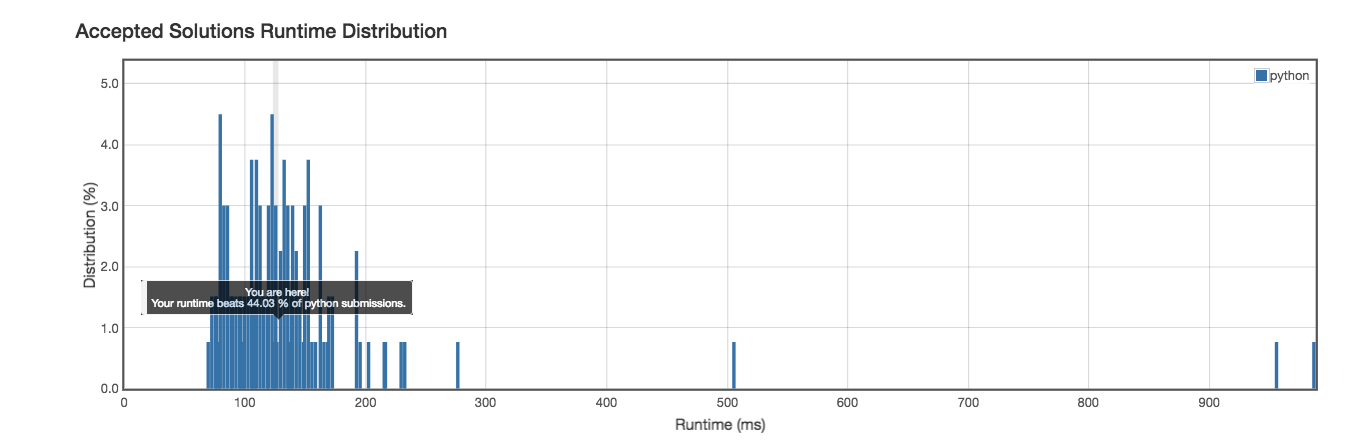imgRuntime: 126ms