Description,
Given a picture consisting of black and white pixels, find the number of black lonely pixels.

The picture is represented by a 2D char array consisting of ‘B’ and ‘W’, which means black and white pixels respectively.

A black lonely pixel is character ‘B’ that located at a specific position where the same row and same column don’t have any other black pixels.

Example:

Input: 
[['W', 'W', 'B'],
 ['W', 'B', 'W'],
 ['B', 'W', 'W']]

Output: 3

Explanation: All the three ‘B’s are black lonely pixels.

The leetcode link

Soace Complexity O(m+n)

Two passes of the matrix.
First pass: build the auxiliary table.
Second pass: do the counting.

Time complexity: O(n)

Runtime: 996ms

class Solution(object):
    def findLonelyPixel(self, picture):
        """
        :type picture: List[List[str]]
        :rtype: int
        """
        ret = 0
        row = [0] * len(picture[0])
        col = [0] * len(picture)
        for i in xrange(len(picture)):
            for j in xrange(len(picture[0])):
                if picture[i][j] == 'B':
                    row[j] += 1
                    col[i] += 1
                    
        for i in xrange(len(picture)):
            if col[i] == 1:
                for j in xrange(len(picture[0])):
                    if picture[i][j] == 'B':
                        if row[j] == 1:
                            ret += 1
        return ret

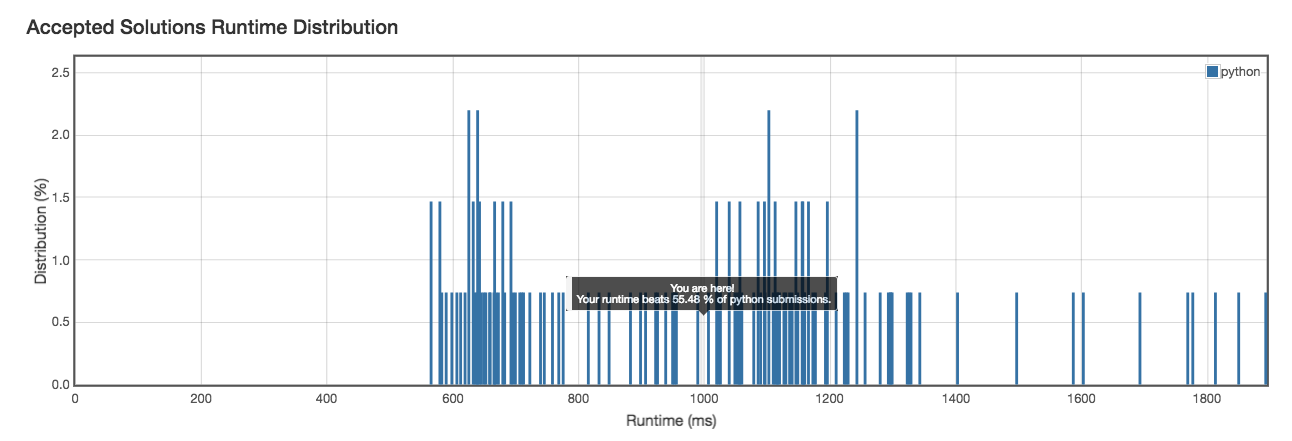imgRuntime: 996ms

Space Complexity O(1)

Two passes of the matrix.
First pass: does not create the auxiliary table, instead, store the auxiliary table’s info into the 1st row and 1st col.
Second pass: do the counting.

Note: the chr(int) will wrap round when it reaches 255, so we need to set a ceiling of ‘Z’ to avoid that.

Time Complexity: O(n)

public class Solution {
    /**
    * @solution:       two pass solution
    * @runtime:        39ms
    * @timeComplexity: O(n) (n = num of elements in matrix)
    * @spceComplexity: O(1)
    */
    public int findLonelyPixel(char[][] picture) {
        int firstColCount = 0;
        int ret = 0;
        for (int i=0; i<picture.length; i++) {
            for (int j=0; j<picture[0].length; j++) {
                if (picture[i][j] == 'B') {
                    if (j == 0) {
                        firstColCount++;
                        if (picture[0][j] != 'Z') picture[i][0]++;
                    } 
                    else {
                        if (picture[0][j] != 'Z') picture[0][j]++; // use 1st row to store "B" count for that col
                        if (picture[i][0] != 'Z') picture[i][0]++; // use 1st col to store "B" count for that row
                    }
                }
            }
        }
            
        for (int i=0; i<picture.length; i++) {
            if (picture[i][0]=='X' || picture[i][0]=='C') {
                for (int j=0; j<picture[0].length; j++){
                    if (picture[i][j] == 'B' || picture[i][j] == 'C') {
                        if (j == 0) {
                            if (firstColCount==1)  ret++;
                        }
                        else{
                            if ((picture[0][j]=='X' || picture[0][j]=='C')) ret++;
                        }        
                    }    
                }   
            }
        }
            
        return ret;
            
    }
}

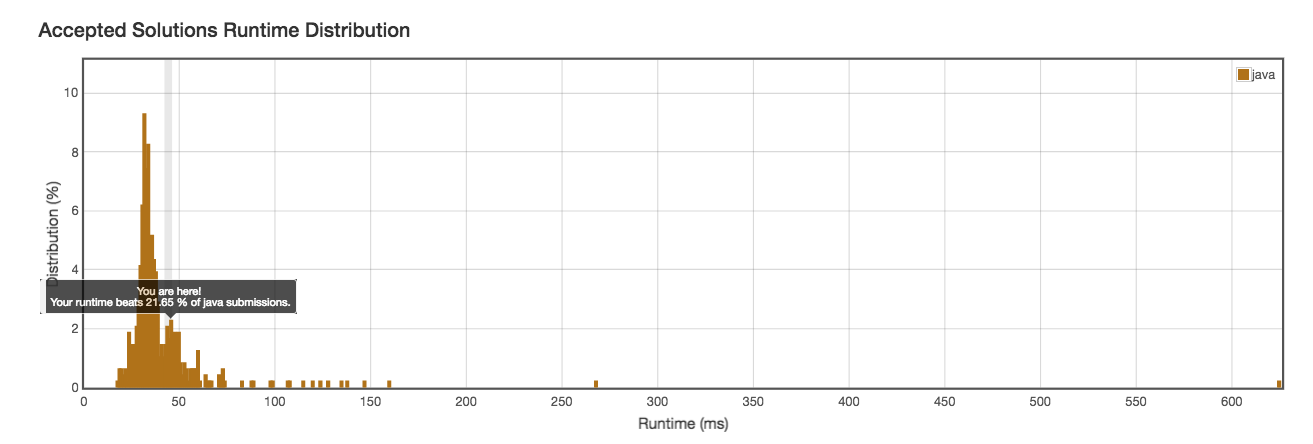imgRuntime: 39ms