Description,
Given an integer array, find three numbers whose product is maximum and output the maximum product.

Example 1:

Input: [1,2,3]
Output: 6

Example 2:

Input: [1,2,3,4]
Output: 24

Note:
The length of the given array will be in range [3,104] and all elements are in the range [-1000, 1000].
Multiplication of any three numbers in the input won’t exceed the range of 32-bit signed integer.

O(n) time complexity solution

Algorithm:

We need not necessarily sort the given numsnums array to find the maximum product. Instead, we can only find the required 2 smallest values(min1min1 and min2min2) and the three largest values(max1, max2, max3max1,max2,max3) in the numsnums array, by iterating over the numsnums array only once.

At the end, again we can find out the larger value out of min1min1xmin2min2xmax1max1 and max1max1xmax2max2xmax3max3 to find the required maximum product.

Note
I used PQ to get the largest nums, instead of single scan, because required to get the top 100 largest nums, PQ will be handy(logn insertion instead of the O(n) insertion of single scan).

public class Solution {
    public int maximumProduct(int[] nums) {
        /**
        * Use PQ to get the top 3 largest nums;
        */
        PriorityQueue<Integer> queue = new PriorityQueue<Integer>(3);
        for (int num : nums) {
            if (queue.size() == 3) {
                if (num > queue.peek()) {
                    queue.poll();
                    queue.add(num);
                }

            } else {
                queue.add(num);
            }
        }
        
        int[] topThreeMax = new int[3];
        int i = 0;
        for (int aNum : queue) {
            // System.out.println(aNum);
            topThreeMax[i] = aNum;
            i++;
        }
        
        /**
        * Use Single Scan to get the two smallest ints.
        */
        int min1 = Integer.MAX_VALUE, min2 = Integer.MAX_VALUE;
        for (int num : nums) {
            if (num < min1) {
                min2 = min1;
                min1 = num;
            }
            else if (num < min2) {
                min2 = num;
            }
        }    
        int largest = Math.max(topThreeMax[0], Math.max(topThreeMax[1], topThreeMax[2]));
        return Math.max(topThreeMax[0]*topThreeMax[1]*topThreeMax[2], largest*min1*min2);
    }
}

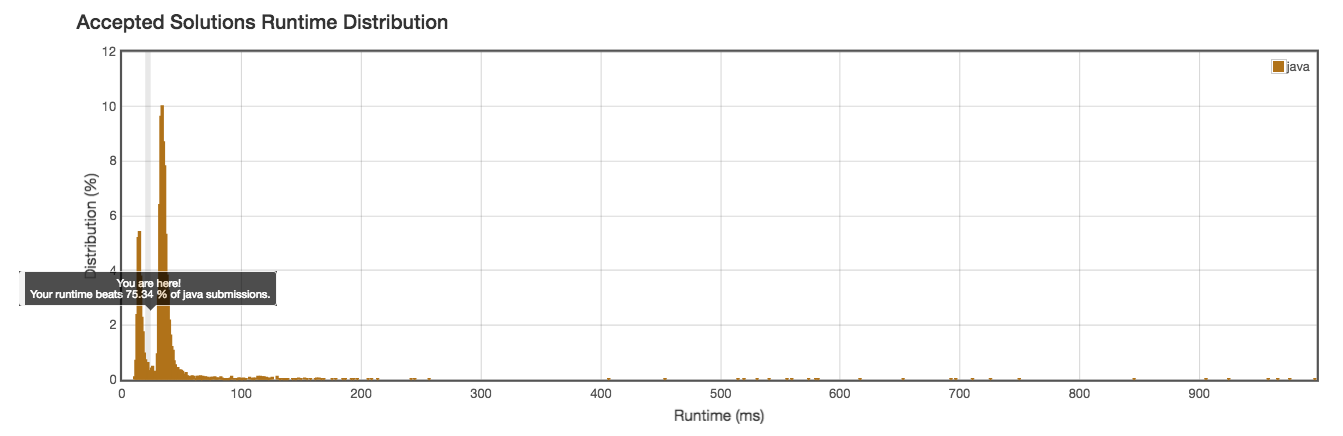imgRuntime: 18ms (Interestingly fall into the gap of O(n) and O(nlogn) solutions because of the overhead of PQ)

Sorting solution

class Solution(object):
    def maximumProduct(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        nums.sort()
        tailMax = 1
        headMax = nums[len(nums)-1]
        for i in xrange(len(nums)-1, len(nums)-4, -1):
            tailMax *= nums[i] 
        for j in xrange(2):
            headMax *= nums[j]
        return max(headMax, tailMax)

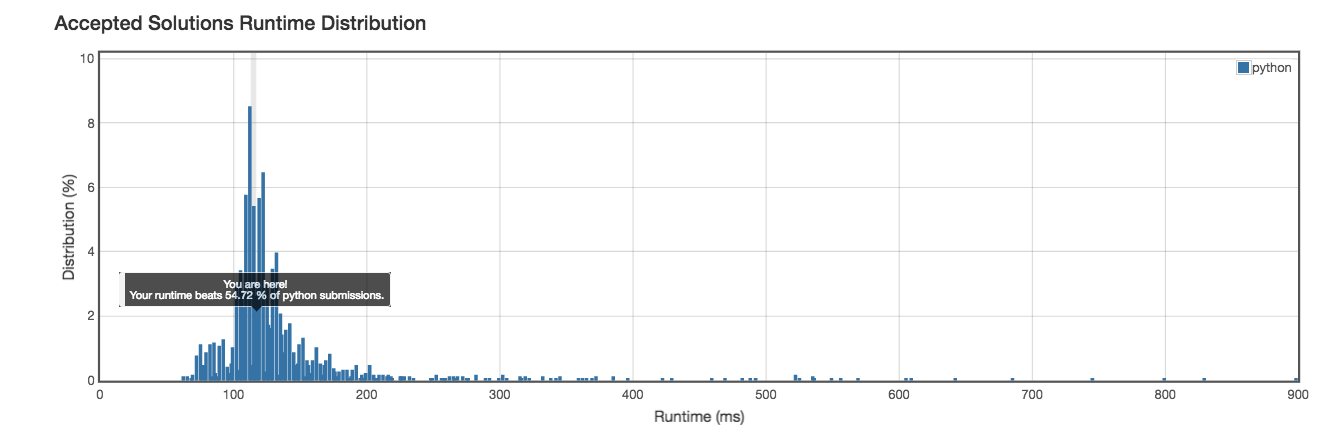imgRuntime: 118ms