Description
You need to construct a binary tree from a string consisting of parenthesis and integers.
The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis. The integer represents the root’s value and a pair of parenthesis contains a child binary tree with the same structure.
You always start to construct the left child node of the parent first if it exists.
Example:
Input: "4(2(3)(1))(6(5))"
Output: return the tree root node representing the following tree:
4
/ \
2 6
/ \ /
3 1 5
Note:
There will only be ‘(‘, ‘)’, ‘-‘ and ‘0’ ~ ‘9’ in the input string.
An empty tree is represented by “” instead of “()”.
O(n) Bottom-up Post-order DFS in Java
Detailed explaination, see here
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
private int i = 0; // make i global
public TreeNode str2tree(String s) {
if (s.equals("")) return null;
return dfs(s);
}
private TreeNode dfs(String s){
TreeNode root = null;
if (s.charAt(i) != '(') {
root = new TreeNode(getIntVal(s));
}
TreeNode leftNode = null, rightNode = null;
if (i < s.length() && s.charAt(i) == '(') { // for the possible leftNode, if '(' met.
i++;
leftNode = dfs(s);
}
if (i < s.length() && s.charAt(i) == '(') { // for the possible rightNode, if '(' met.
i++;
rightNode = dfs(s);
}
// if not '(' it must be ')' or i==s.length()
// so we return the current stack
root.left = leftNode;
root.right = rightNode;
i++;
return root;
}
private int getIntVal(String s) {
StringBuilder sb = new StringBuilder();
while (i < s.length()) {
if (s.charAt(i) == '(' || s.charAt(i) == ')')
break;
sb.append(s.charAt(i));
i++;
}
int val = Integer.valueOf(sb.toString());
return val;
}
}
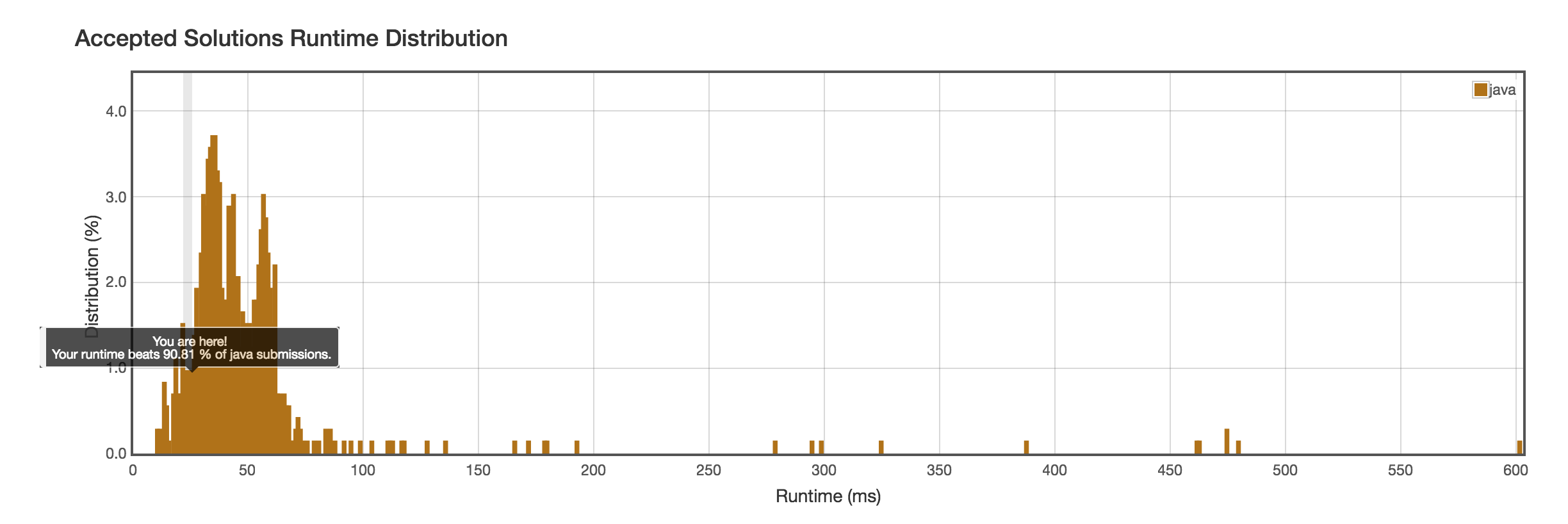 Runtime: 18ms
Runtime: 18ms