Description,
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

Example:

Given nums = [-2, 0, 3, -5, 2, -1]

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

Note:
You may assume that the array does not change.
There are many calls to sumRange function.

The cumulative (caching) solution

Because the query will be used very frequently, you will need to cache the results using hashmap, or do a pre-computation.
Solution below is a pre-computation one,

Time complexity : O(1) time per query, O(n) time pre-computation. Since the cumulative sum is cached, each sumRange query can be calculated in O(1) time.
Space complexity : O(n).

class NumArray(object):
    """
    The cumulative (caching) solution
    @timeComplexity: O(n)
    @runtime:        68ms
    """

    def __init__(self, nums):
        """
        :type nums: List[int]
        """
        self.nums = nums
        self.sums = [0] * len(nums)
        prevSum = 0
        for i in xrange(len(nums)):
            self.sums[i] = prevSum + nums[i]
            prevSum = self.sums[i]
        

    def sumRange(self, i, j):
        """
        :type i: int
        :type j: int
        :rtype: int
        """
        
        if i == 0:
            return self.sums[j]
        else:
            return self.sums[j] - self.sums[i-1]
        


# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# param_1 = obj.sumRange(i,j)

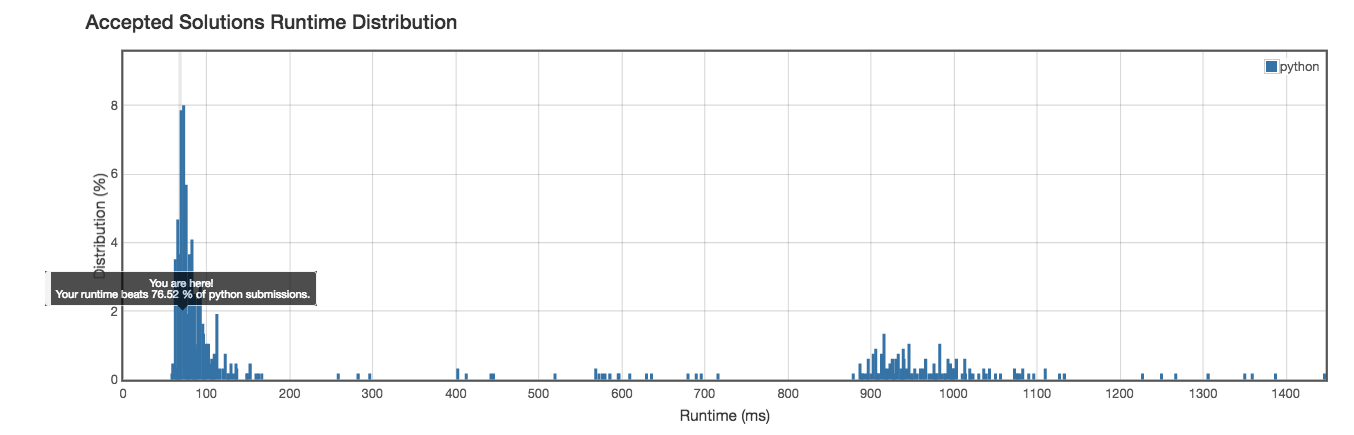imgRuntime: 68ms