Description,
Write a function that takes an unsigned integer and returns the number of ’1’ bits it has (also known as the Hamming weight).

For example, the 32-bit integer ’11’ has binary representation 00000000000000000000000000001011, so the function should return 3.

leetcode link

Loop and Mask

The solution is straight-forward. We check each of the 32 bits of the number. If the bit is 1, we add one to the number of 1-bits.

We start with a mask m=1, because the binary representation of 1 is,

0000 0000 0000 0000 0000 0000 0000 0001

Clearly, a logical AND between any number and the mask 1 gives us the least significant bit of this number. To check the next bit, we shift the mask to the left by one.

0000 0000 0000 0000 0000 0000 0000 0010

class Solution(object):
    def hammingWeight(self, n):
        """
        :type n: int
        :rtype: int
        """
        count = 0
        mask = 1
        for _ in xrange(32):
            if n & mask != 0:
                count += 1
            mask <<= 1
            
        return count

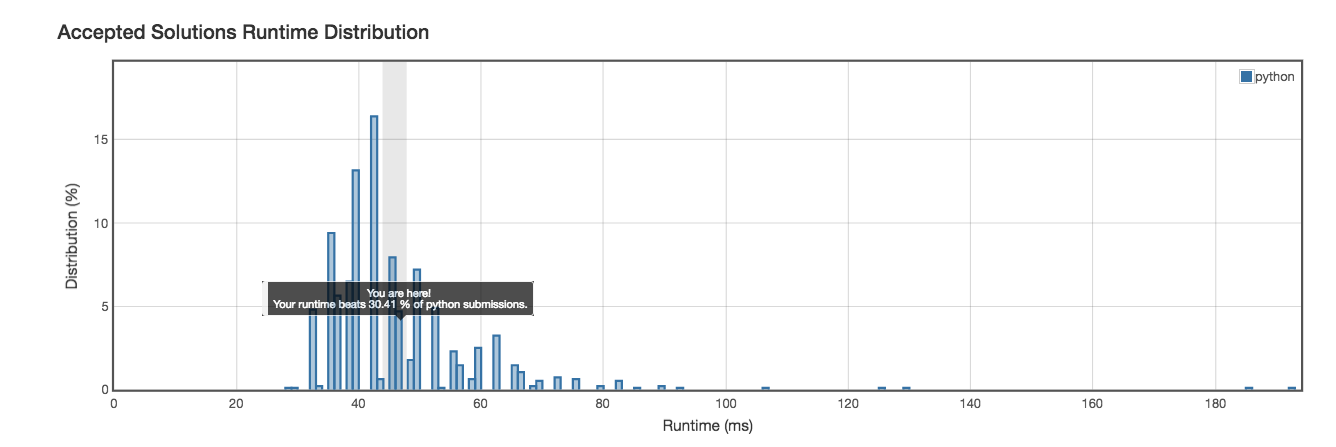imgRuntime: 46ms

Flip and Cancel

We can make the previous algorithm simpler and a little faster. Instead of checking every bit of the number, we repeatedly flip the least-significant 1-bit of the number to 0, and add 1 to the sum. As soon as the number becomes 0 we know that it does not have any more 1-bits, and we return the sum.

The key idea here is to realize that for any number n, doing a bit-wise AND of n and n−1 flips the least-significant 1-bit in n to 0.

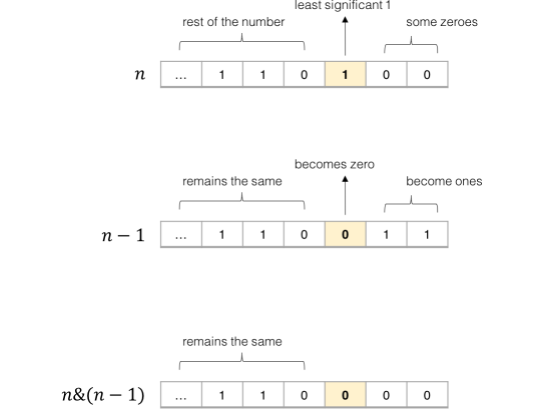imgn = n&(n−1) flips the least-significant 1-bit to 0

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        /**
        * Flip and cancel the least-significant "1"
        * @runtime:        2ms
        * @timeComplexity: O(1) -- constant time
        */
        int count = 0;
        while (n != 0) {
            count++;
            n &= (n-1);
        }
        return count;
    }
}

imgRuntime: 2ms